How to Play
Create a path through the grid from "in" to "out". Every square included in the path must have exactly 2 walls. No other walls are allowed in the grid.
The numbers to the right of each row are the total number of walls for that row. The numbers at the bottom of each column are the total number of walls for that column.
Clues
Each Domaji puzzle contains clues to help you start the puzzle off. In addition, some puzzles may already have walls set. The clues are described below.
 |
The "included" clue. This clue indicates that the square is included in the path. |
 |
The "excluded" clue. This clue indicates that the square is not included in the path. |
 |
The "pass-through" clue. This clue indicates that the path passes between the two squares on either side of it. |
 |
The "one-side-only" wall clue. This clue indicates that one of the squares beside the wall is included in the path and the other is not. Because this clue is a wall, it counts towards the total wall count for the row or column. |
Getting Started
The best way to start a Domaji puzzle is to complete the obvious walls first. Usually there will be some obvious walls near the edge of the puzzles and some within the grid. Here are a few core tips that will get you started.
One side only clue
One of the best clues that is present on a Domaji puzzle is a one-side-only wall clue. This clue indicates that the path that travels from the "in" to "out" will pass on one side of the wall only and it counts towards the wall count for the row or column.
If it is known that a square is included on one side of a one-side-only clue, then the square on the other side of the wall must be excluded. Conversely, if it is known that a square is excluded on one side of a one-side-only rule, the the square on the other side must be included.
In the example below, there is a one-side-only wall between the two upper squares.
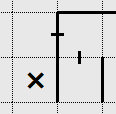
The square to the left of the one-side-only wall is initially unknown, but because there is a pass-through hint on the right square, the left square must be excluded.
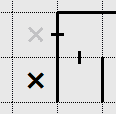
Two on/two off rule
This rule is core to Domaji. All squares that are included in the path must have two walls. The other two "slots" are where the path enters and exits the square.
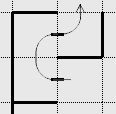
Taking the following set of squares, the two on/two off rule can be applied to complete 3 of the squares.
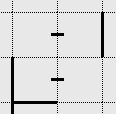
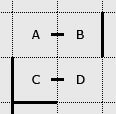
Labelling the squares A to D, the following can be determined:
- Square C already has two on/two off.
- The slot between squares A and C is clear and the slot between is squares A and B is clear. With two of the slots surrounding square A cleared the remaining two slots must be walls.
- The slot between squares B and D cannot be off. If it were, a loop would be created. Consequently that slot must be a wall.
The result is that 3 initially unknown slots are confirmed as walls.
Included edge squares
If a square on the edge of the puzzle is included in the path and that square is neither an exit nor entry square, then the edge slot for that square is always a wall. Conversely, if an edge slot is a wall then the associated square is always included in the path.
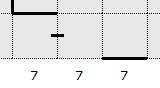
In the example above, two of the edge squares are included in the path by virtue of the pass-through hint between the squares. The third square has an edge wall and is thus included in the path also. What cannot be determined from this is whether the three squares are sequentially connected, but at least the two edge slots are confirmed walls.
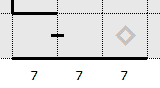
A consequence of an included square being present on the edge of the puzzle is that there must be at least two of them on the edge side by side. This is a useful rule to quickly find included edge squares.
The following example shows the upper edge of a puzzle containing a wall perpendicular to the edge and one included square on either side of the wall.
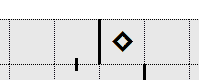
In this example, the edge squares on either side of the known included edge squares must also included, and thus their edge slots are confirmed walls.
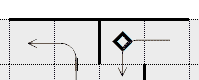
Included corner squares
If a corner square is included in the path, and it or its surrounding edge squares are neither an "in" nor "out" square, then the two surrounding edge squares must also be included in the path.
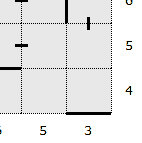
As in the example above, the corner square is included in the path if one of its edge slots are walls. It may also be included in the path if this has been determined using another technique.
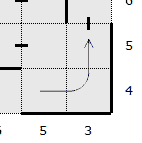
Completed lines
Once a line has been completed, it is often possible to identify how the path travels through the line. If this can be identified, then it may additionally be possible to complete some of the walls surrounding the squares in the line.
|
|
The left and right walls of the top square in the sequence cannot be altered because it is not possible to determine whether the path enters the top square from the left or the right. This example also shows a 2 square sequence near the bottom, but again it is not yet possible to determine which of the left and right slots from these squares should become walls. |
Impossible wall locations
This advanced technique provides a means to find the state of one or more walls simultaneously. This technique is required more and more as the puzzles get harder in grading.
|
|
The purpose of this technique is to eliminate as many wall slots as possible. If few enough slots remain, it may be possible to determine with certainty that one or more walls should be placed in certain remaining slots. For example, if it were possible to eliminate 4 of these 7 slots, then we'd be left with 3 slots into which we could place the remaining 3 walls directly. |
|
Underneath the excluded square is a single square that must also be excluded because the path requires two free slots through which to travel through a square and this square doesn't meet this requirement. These two excluded squares clear slots D and E because walls cannot be placed between excluded squares. The square below wall E has been identified as excluded from the path. On the bottom side of this square is a one-side-only clue, which tells us that the square underneath it is included in the path. This square already has two walls, so the remaining slots must be cleared, thus slot F can be cleared. We're now left with slots A, B, C and G - 4 slots into which 3 walls must be placed. |
Given that there are only two more slots available we know with certainty that slots A and G must be walls. We don't know which of slots B or C is a wall, so for the time being, these are left undetermined. |
Guided Tour
This guided tour steps through a typical Domaji puzzle. If this guide is not enough for you, check out detailed solution steps for an example Domaji puzzle.
At the start of the puzzle, we’ll be using the techniques discussed in the Getting Started section.
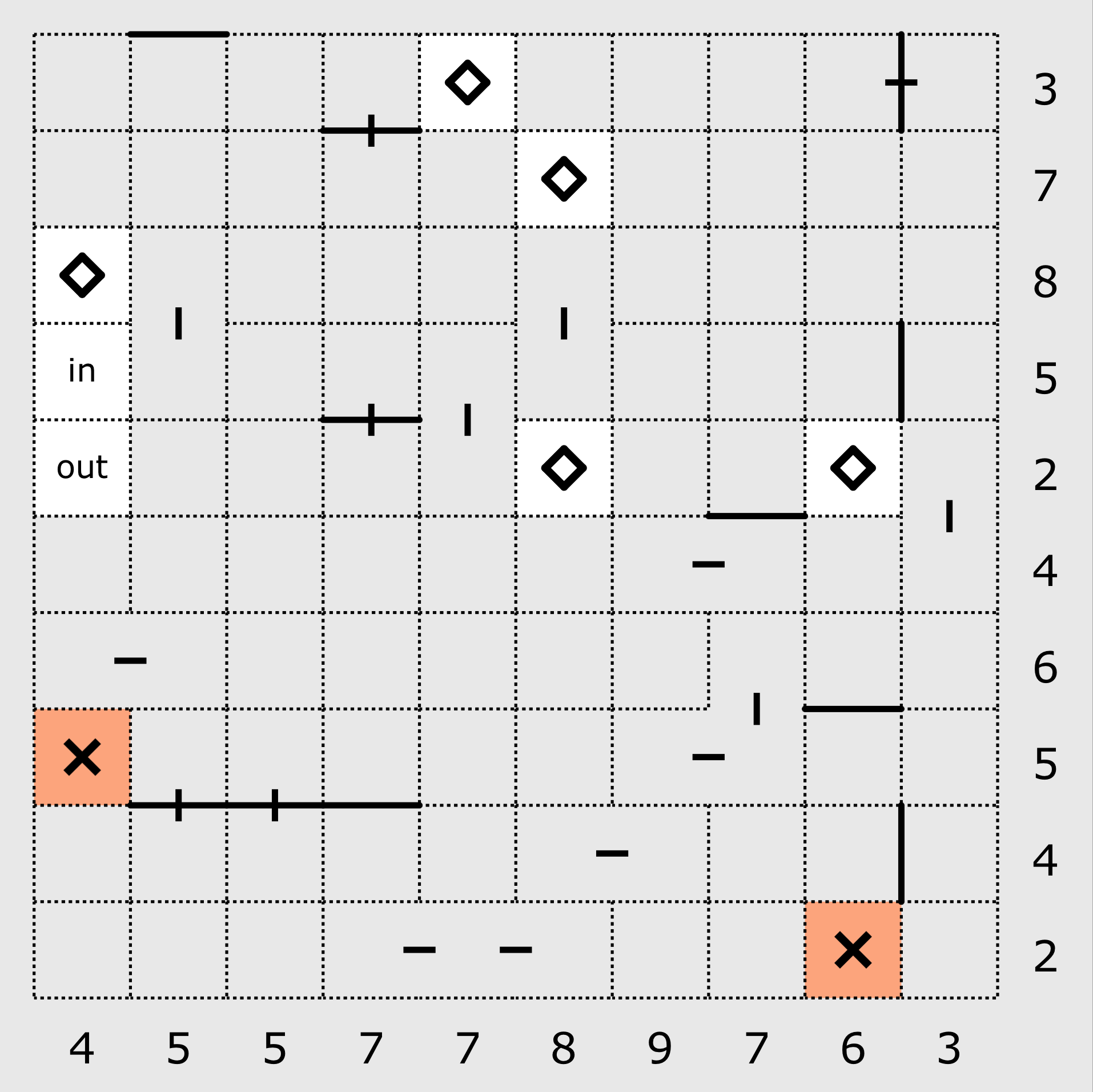
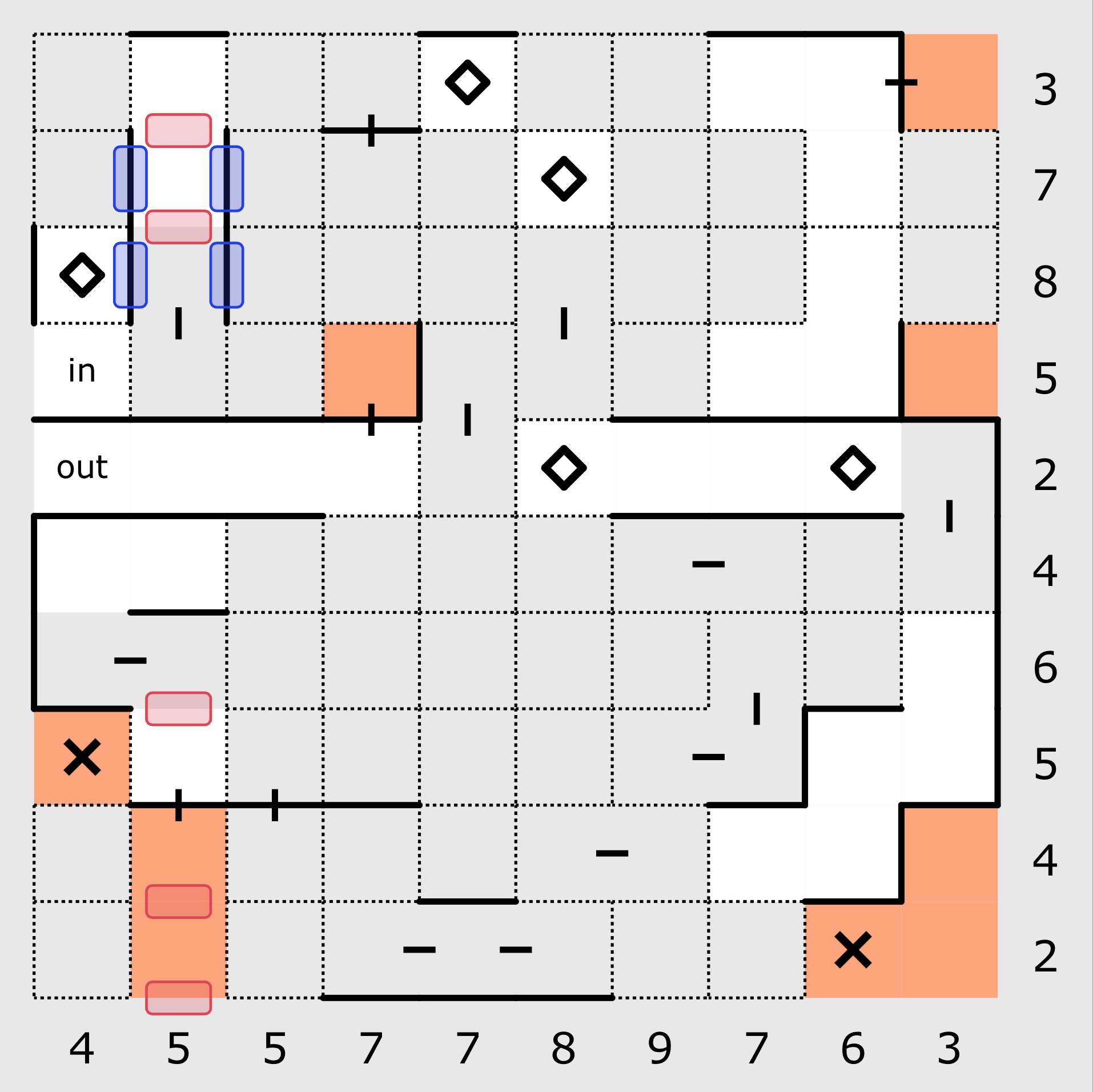
The sample puzzle above is a 10x10 puzzle, which means that the number of "slots" available for you to place walls in each row and column is 11. At the beginning, there will be a set of clues to get you started. Some of the walls that result from these clues are immediately visible.
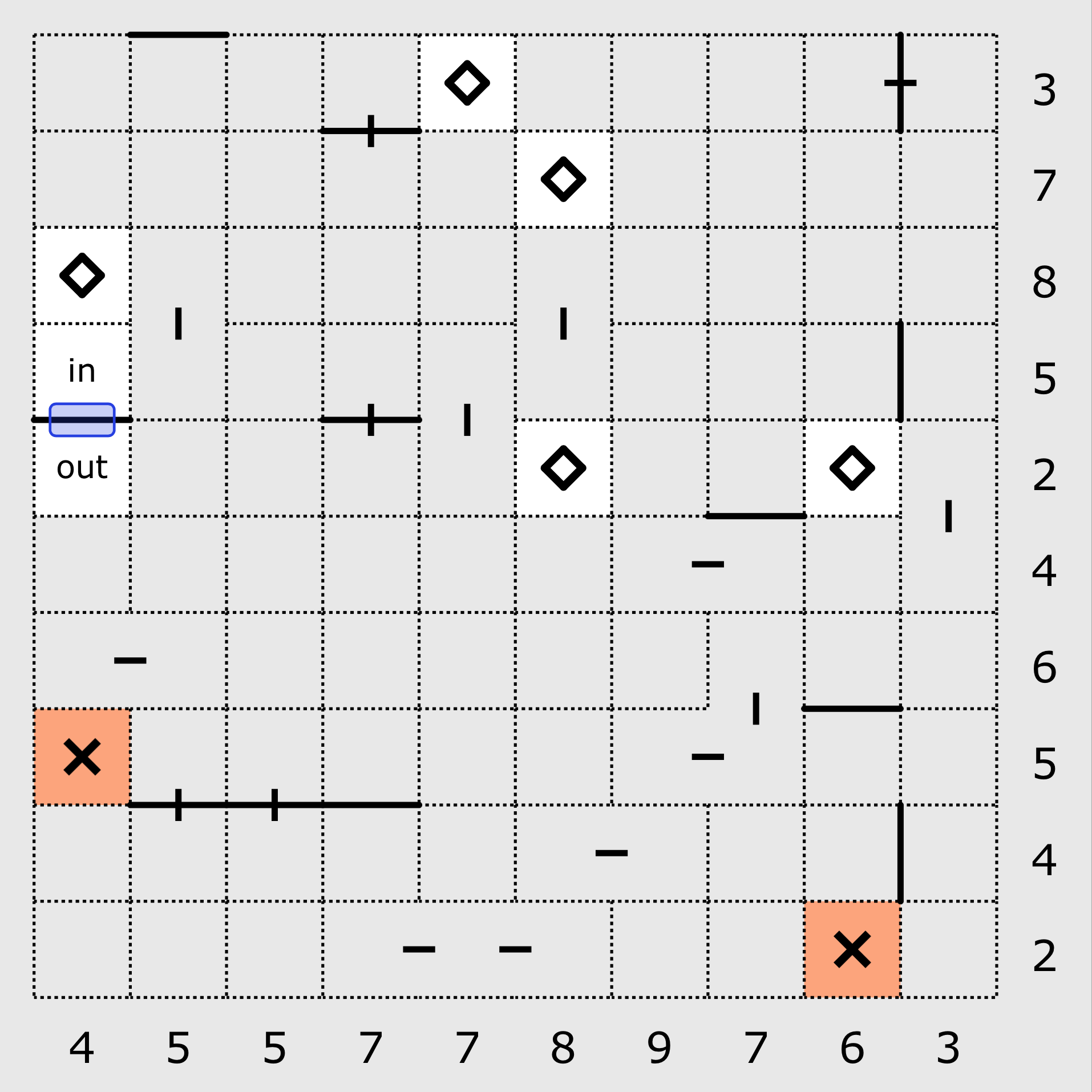
Because the "in" and "out" squares in this puzzle neighbour one another, one of the most obvious walls in this puzzle sits between these two squares. If there was no wall between these squares, the path would be very short!
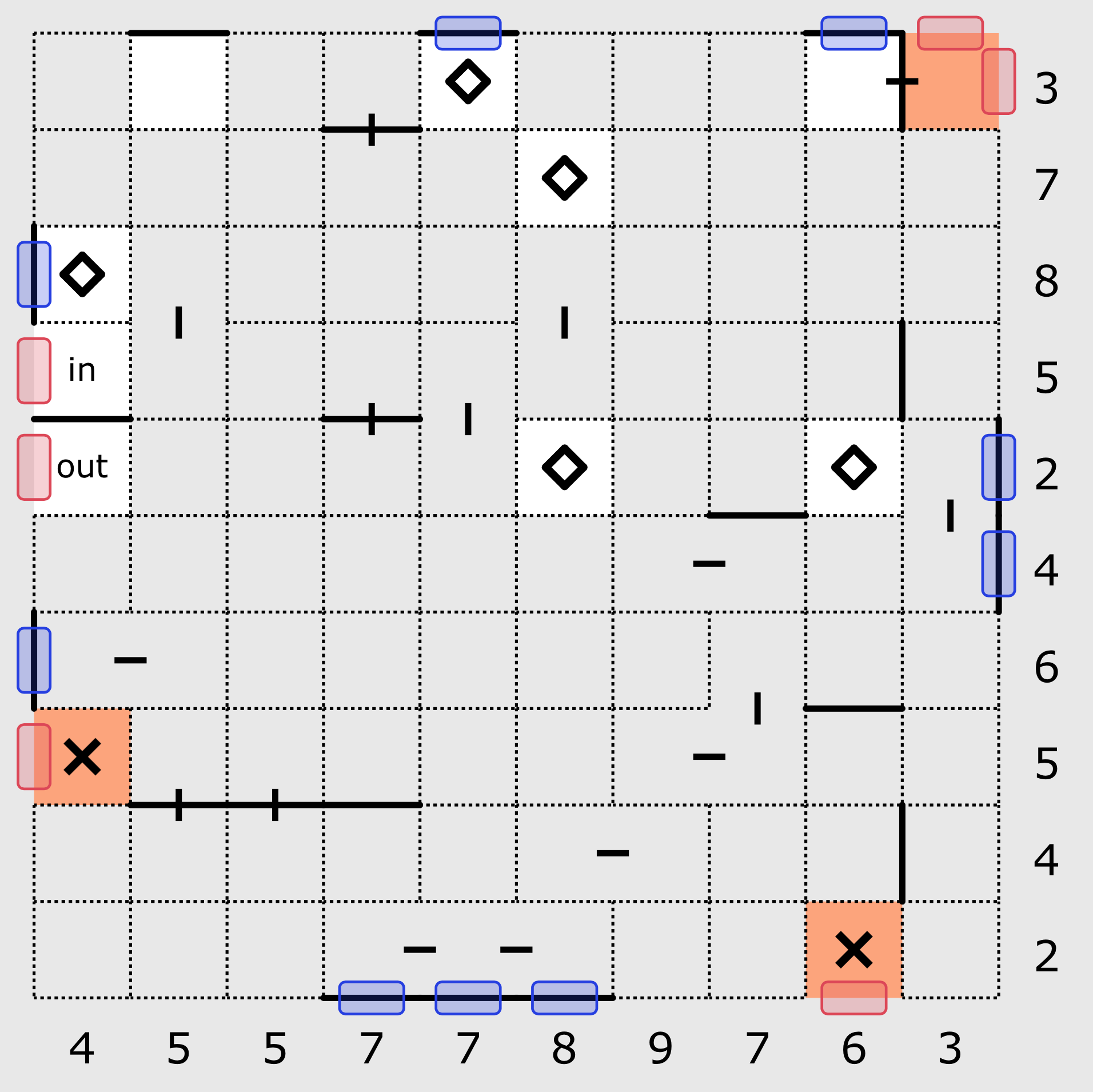
In almost all Domaji puzzles, there will be some clues near the edge of the puzzle that immediately allow you to place some walls (highlighted in blue above). In addition to the walls that can be quickly placed on the edge of the puzzle, it is also possible to eliminate some slots (highlighted in red above) from being capable of containing a wall if the square beside the slot on the edge is excluded from the path. Remember that the more slots that cannot contain a wall on a given row or column, the closer you get to finding the location of the walls that do get placed.
Note that the edge slots for the "in" and "out" squares cannot contain a wall (highlighted in red above).
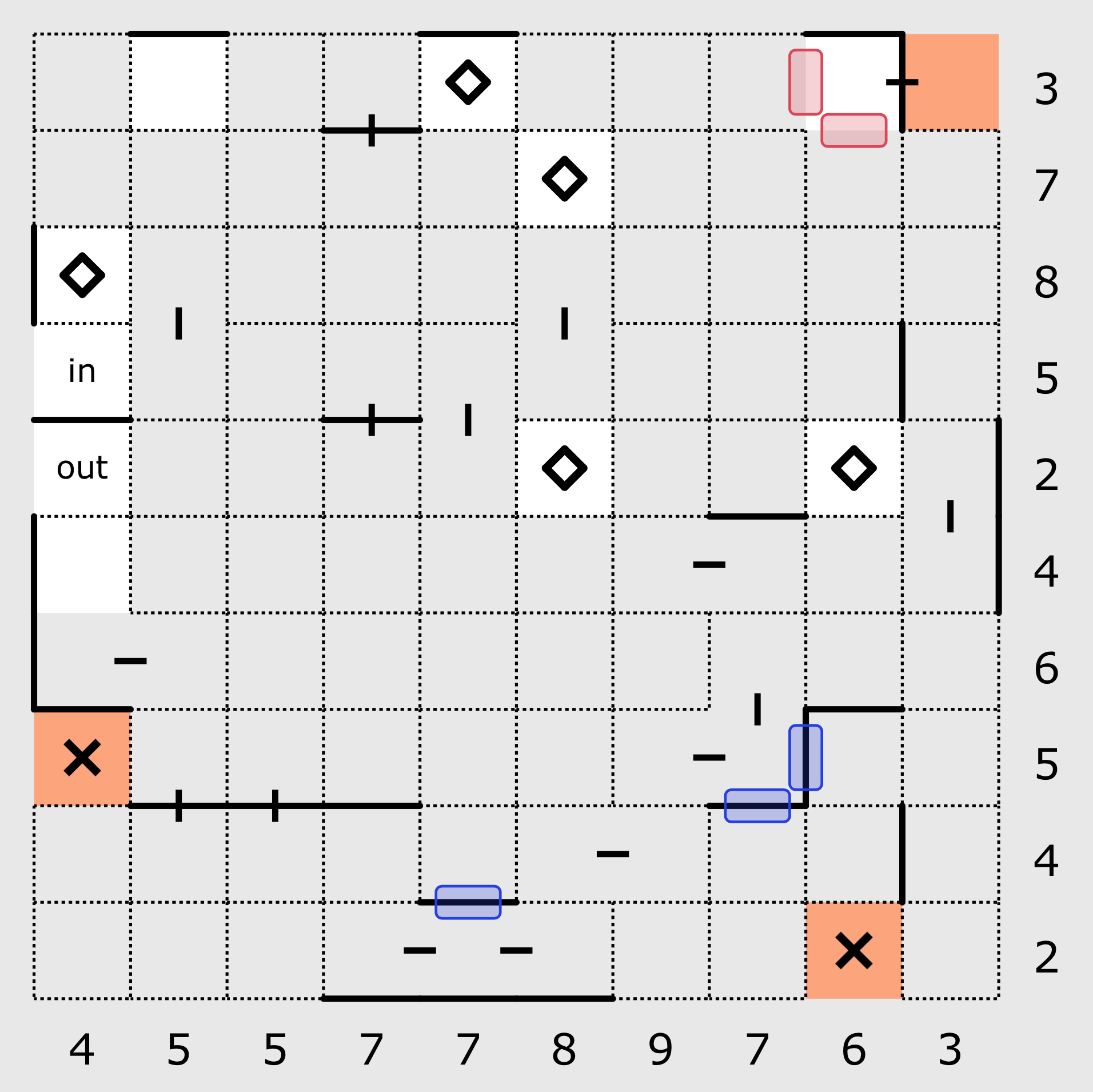
One of the fundamental rules of Domaji is that any square that is included in the path must have exactly two walls. Because all squares in the grid have 4 possible slots, if an included square already has 2 slots where the path is passing through, then the other two slots must contain walls (highlighted in blue above). Similarly, if an included square already has two walls, then the other two slots cannot contain walls and thus the path must be passing through those slots (highlighted in red above).
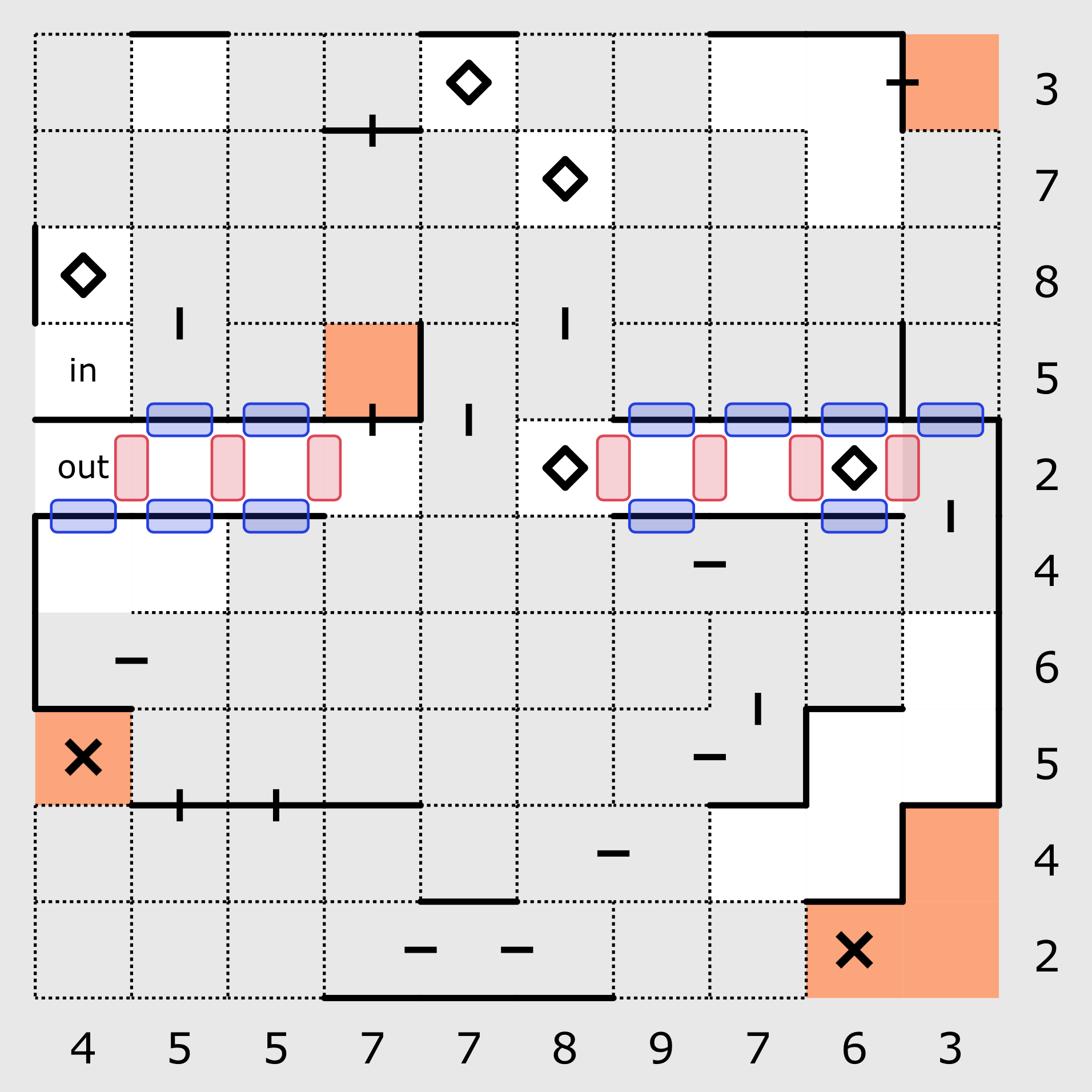
The square above, 5 in from the left and 5 down from the top has a pass-through clue in its top slot. The total number of walls on the horizontal row containing the square is 2 and one of those is used up on the right-most slot. This leaves only one wall remaining. This square tells us into which slots the remaining wall cannot be placed.
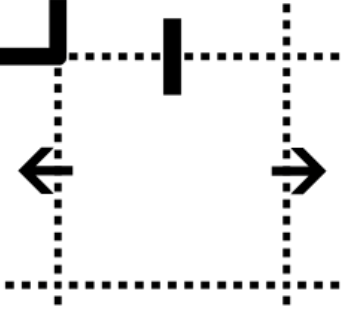 The
path is passing through the slot at the top of the square and must be travelling either right or left. It cannot
be travelling downwards because that would result in the square having a wall on both the left and the right,
which would subsequently result in the row having 3 walls instead of 2.
The
path is passing through the slot at the top of the square and must be travelling either right or left. It cannot
be travelling downwards because that would result in the square having a wall on both the left and the right,
which would subsequently result in the row having 3 walls instead of 2.
With the remaining wall located either on the right or left of the square above, we know that all other free slots cannot contain a wall and thus many of the lateral walls within the row can be drawn.
A similar situation occurs above in the second column from the left. In this instance, all 5 walls have been placed so all remaining slots are clear. With this known, the 4 lateral walls highlighted in blue above can be placed.
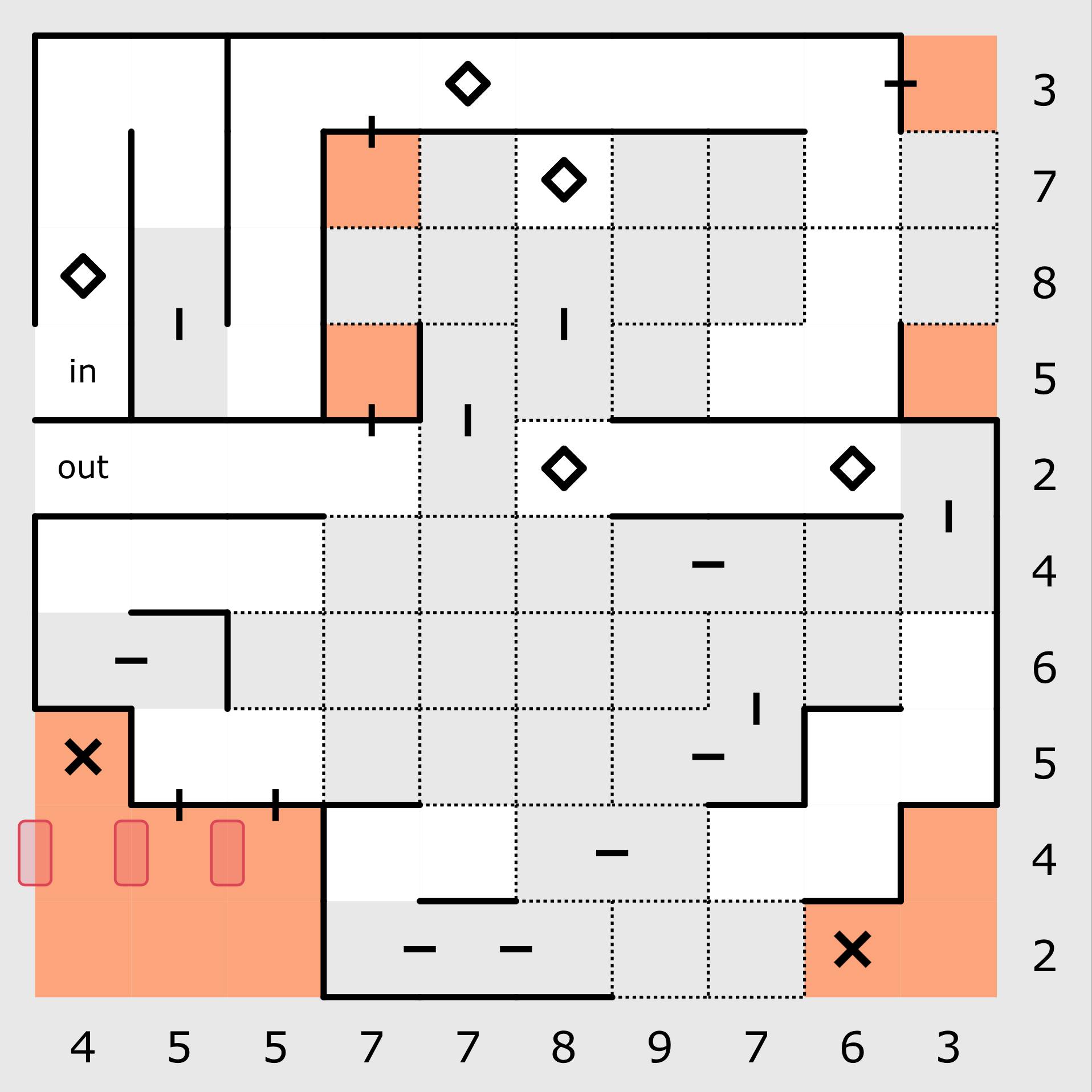
As you complete the puzzle, you will be continually checking the wall counts in each of the rows and columns. In the example above, the second to bottom horizontal row has a total wall count of 4, 2 of which are already placed. The slots that are highlighted in red indicate those into which a wall cannot be placed because they are either between two excluded squares or they are on the edge with an excluded square neighbouring them. There are two other slots into which a wall cannot be placed. Can you find them?
The result is that there are only two slots into which walls can be placed. There are also two walls remaining, so these two remaining walls must be placed into those slots as show below.
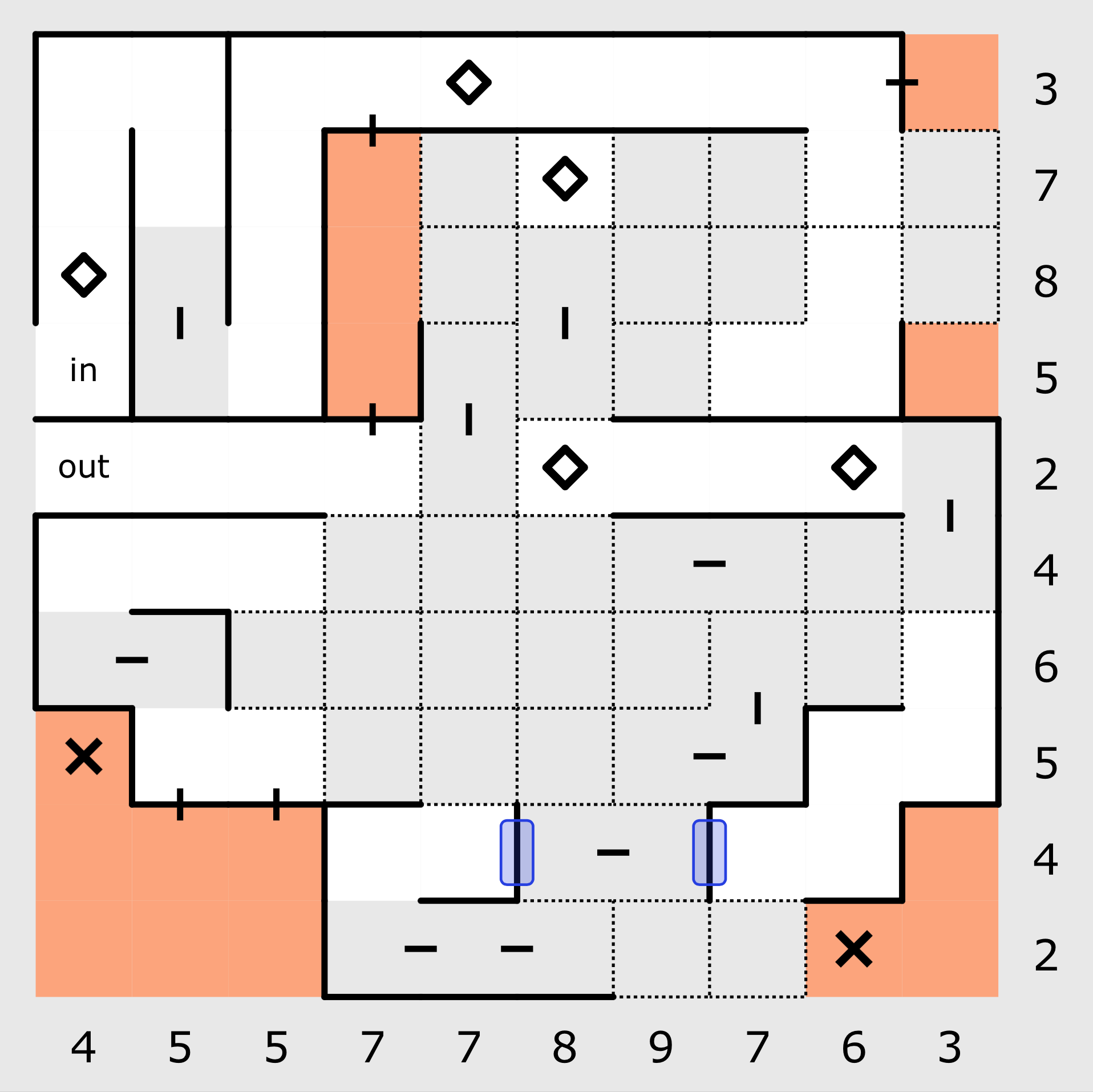
Keep stepping through the puzzle using the same techniques as we’ve discussed in this guided tour and before long you will have solved it. The completed puzzle can be seen below.
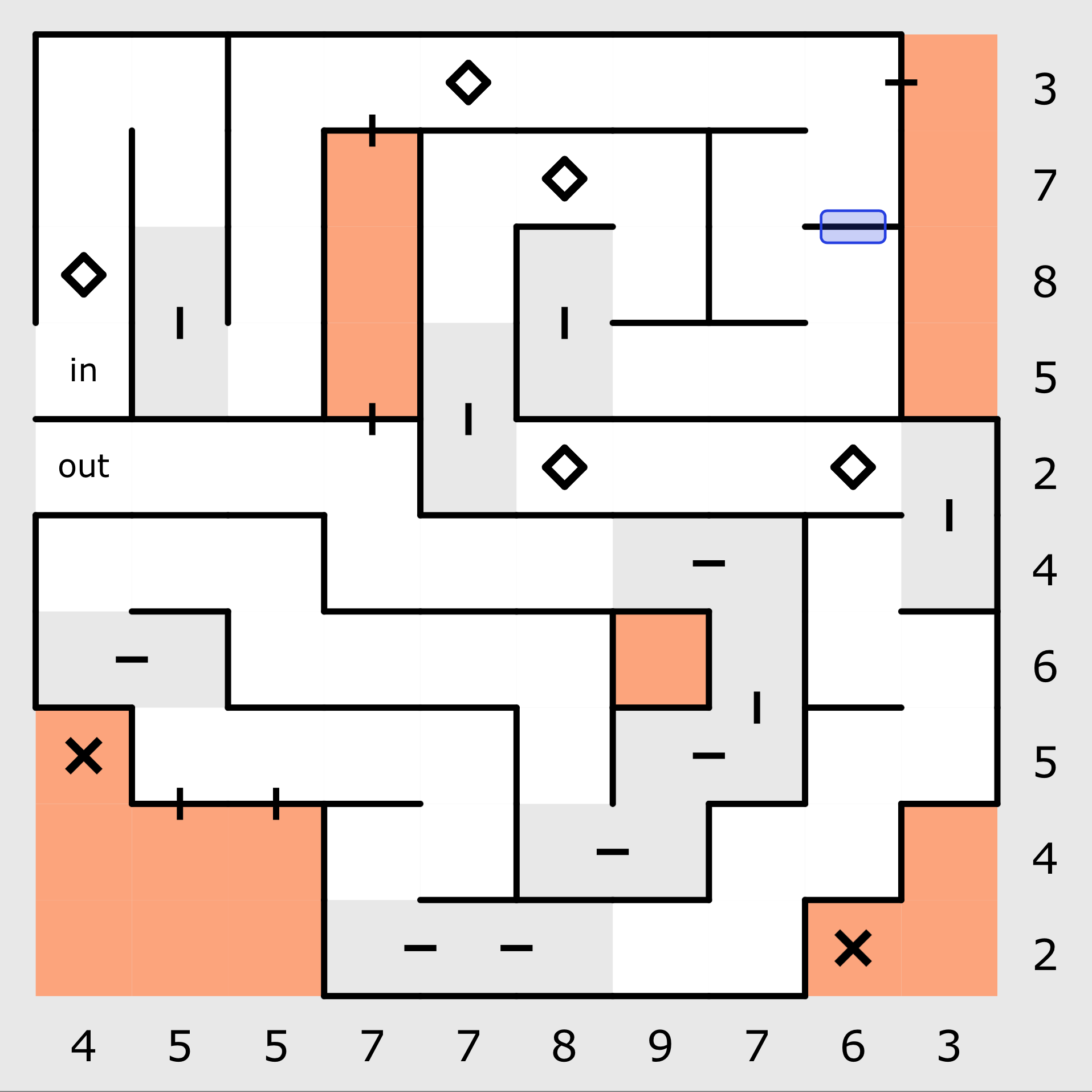

 The completed column to the left contains a
sequence of 4 squares. It is obvious from the included clue at the top of this set of 4 that all 4
squares are included and the path travels along the sequence. If this were not true, then a wall would
need to exist within the set, but given that all walls in this column have been used, another wall
cannot be added.
The completed column to the left contains a
sequence of 4 squares. It is obvious from the included clue at the top of this set of 4 that all 4
squares are included and the path travels along the sequence. If this were not true, then a wall would
need to exist within the set, but given that all walls in this column have been used, another wall
cannot be added.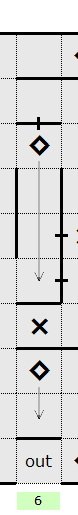 With the 4 squares determined to be in a
sequence, the two inner squares from the sequence have two slots cleared. The other two slots are thus
confirmed walls.
With the 4 squares determined to be in a
sequence, the two inner squares from the sequence have two slots cleared. The other two slots are thus
confirmed walls.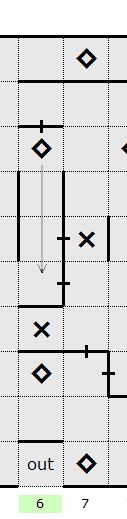 In this example, the column containing a total of 7
walls currently has 4 turned on leaving 3 more walls to place. Using this technique it will be
possible to find the locations of 2 of these three walls.
In this example, the column containing a total of 7
walls currently has 4 turned on leaving 3 more walls to place. Using this technique it will be
possible to find the locations of 2 of these three walls.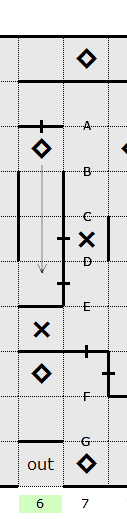 There are 7 available wall slots remaining in
the column. For the purpose of this example, these have been marked A to G.
There are 7 available wall slots remaining in
the column. For the purpose of this example, these have been marked A to G.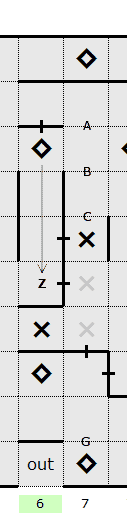 The square marked Z is a good starting point. This
square is included in the path. With the one-side-only hint on the right of the square, the square to
the right can be excluded from the path.
The square marked Z is a good starting point. This
square is included in the path. With the one-side-only hint on the right of the square, the square to
the right can be excluded from the path.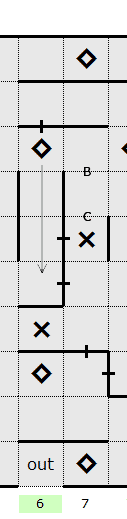 In order to determine which 3 of the 4 slots
the remaining walls must be placed into, we can look at the square between slots B and C. If this
square were included in the path, only slot C could be a wall. Slot B could not be a wall because it
would violate the two on/two off rule. If this square were excluded from the path, only slot B could
be a wall because walls cannot be placed between excluded squares. Consequently only one of either B
or C can be a wall.
In order to determine which 3 of the 4 slots
the remaining walls must be placed into, we can look at the square between slots B and C. If this
square were included in the path, only slot C could be a wall. Slot B could not be a wall because it
would violate the two on/two off rule. If this square were excluded from the path, only slot B could
be a wall because walls cannot be placed between excluded squares. Consequently only one of either B
or C can be a wall.